Understanding the geometry of geologic structures, and how they have grown over time, requires an understanding of the mechanical controls on their evolution. By better understanding the role that rock properties play in their growth we gain the ability to improve our understanding of these systems in both fundamental and applied ways: we can more confidently interpret the first-order geometries of these types of structures in natural settings, helping to improve predictions of subsurface geometries for regional tectonic studies, petroleum exploration, and seismic hazard assessment. We can also use our insight into the distribution of stress and strain within these structures to make better predictions about the distribution of second-order structural features, like small faults and fractures, which have implications for how fluids flow through the rocks in hydrologic and petroleum reservoir applications. Additionally, understanding what types of structures form most easily under realistic geological conditions can help guide our choice of interpretation for natural systems (i.e., knowing that a certain style of structure requires very specific mechanical conditions to form, we can choose to apply such interpretations only when we can be confident that those conditions are met).

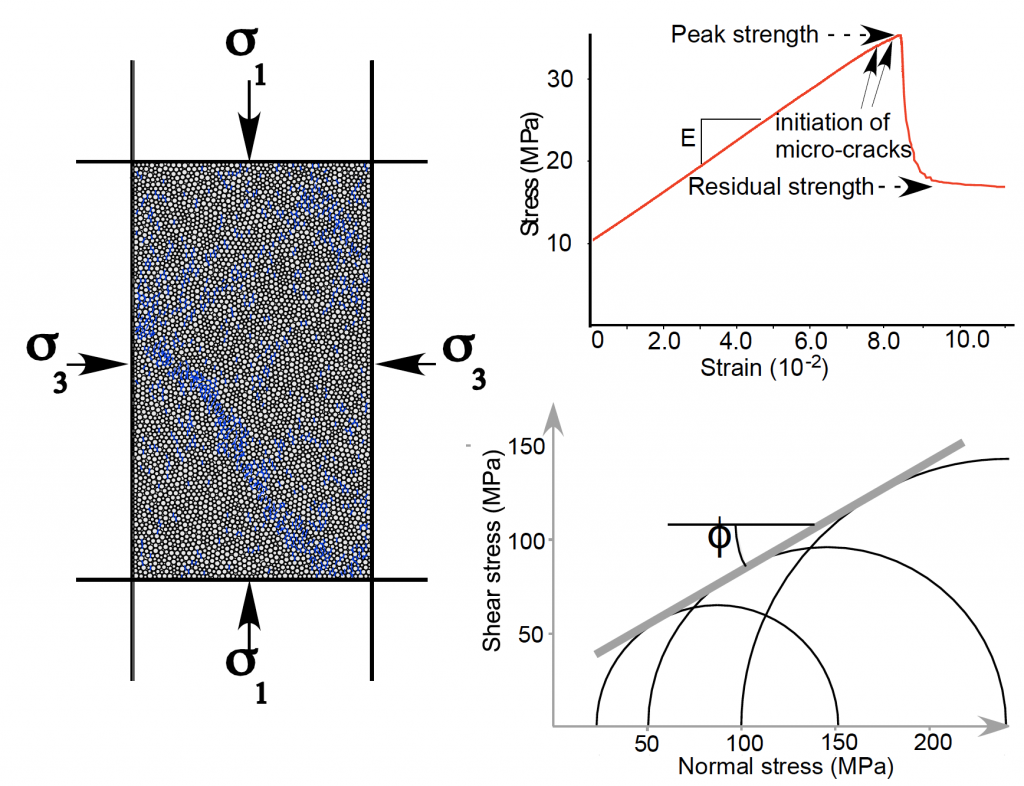
Calibration of micro-scale properties of a discrete element model to match realistic rock properties, though synthetics rock mechanics biaxial strength tests. Left: Image of synthetic rock mass, with blue showing broken inter-particle bonds (fractures) at the point of failure for the sample. Right: Evolution of stress and strain at a given confining stress, and failure at different confining stresses, permit observation of bulk modulus (E) and coefficient of internal friction (phi) approximated by this combination of micro-properties (from Hughes, 2020).

In our group, we have several past and ongoing projects aimed at understanding the styles of structures that form under specific mechanical conditions in both shortening and extensional environments. By varying the mechanical properties of the rock package that is deforming, the contrast in strength between rock layers, the rate at which the rocks are strained, and the boundary conditions, we are able to use numerical mechanical modeling to evaluate the styles of structures that emerge. We primarily use discrete element modeling, in which the rock mass is approximated as a series of particles that interact with each other at the micro-scale in order to approximate realistic bulk material properties for rocks.

Once the model is run, it can be interrogated in a number of ways; it’s geometric evolution over time can be characterized and compared with kinematic models that describe structures, and the stresses and strains throughout the model history can also be visualized.

The set-up of these models depends upon the hypothesis being tested. In some cases, we aim to test a narrow hypothesis (why do fault-bend or fault-propagation folds form in shortening), and correspondingly, set pretty specific boundary conditions to ensure that the results bear on the question at hand. In other cases, we want to allow for any type of structure to form, so we do not seed anything about the fault geometries (e.g., within a shortening rock mass) in order to learn more about what types of features would intrinsically emerge from such conditions. The choice of DEM to model permits this kind of freedom, as it is well suited to modeling high-strain scenarios without explicitly prescribing the fault geometry.

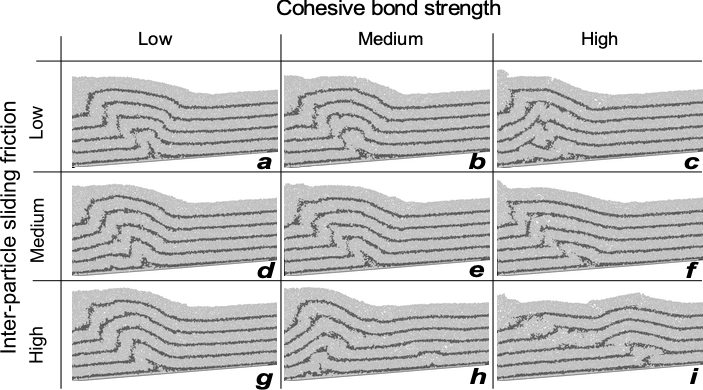
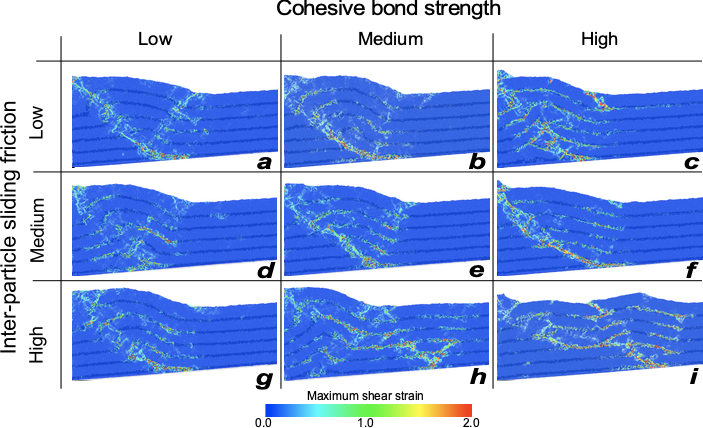
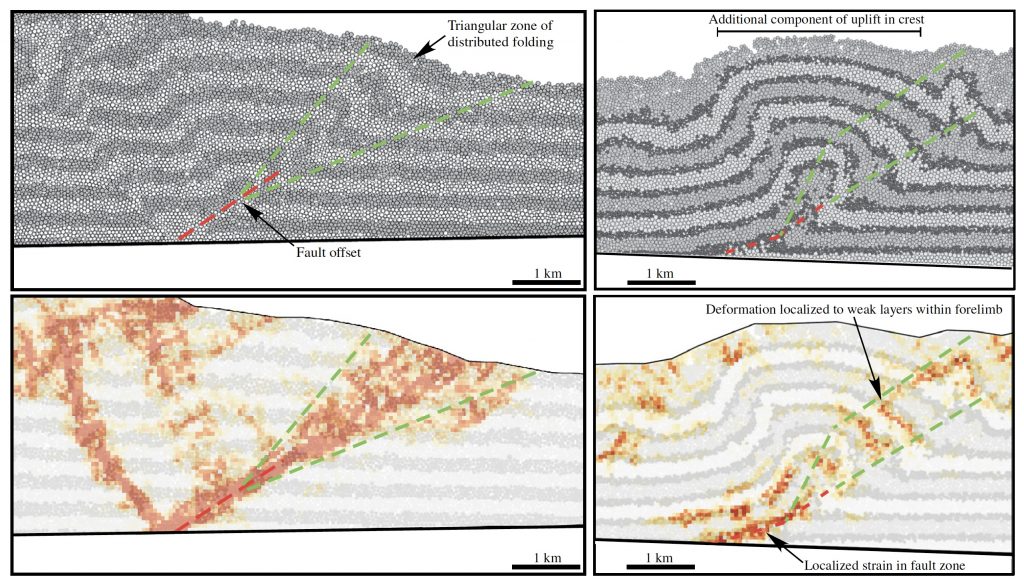
Geometry of models under a variety of mechanical strength conditions emphasizes the role of peak strength (a function of cohesive bond strength) and strain weakening (a function of interparticle sliding friction) on the styles of structures that emerge in shortening wedges (from Hughes, 2020). Model simulation conducted using Itasca PFC.
Visualization of distortional strain during the previous 100 m of shortening, overlain on the model geometry for the previous figure, highlighting the location of faults, distributed shear, and flexural slip along weak layers, that facilitate the growth of the structures within the model (from Hughes, 2020).

Past projects we have completed on this topic have focused on understanding the mechanical conditions that relatively favor fault-bend and fault-propagation folding, as well as more general mechanical controls on structural style at the scale of fold-and-thrust belts. Further work focused on large-scale modeling of fold-and-thrust belts, particularly aimed at quantifying the impact of strain weakening and strain rate on fold and thrust belts, and application to specific fold-and-thrust belt case studies, is ongoing.

Discrete element modeling that demonstrates trishear-style fault propagation folding occurs in more mechanically homogeneous rock masses (left), while kink-style fault-propagation folds occur in more strongly layered rock masses (right) (from Hughes and Shaw, 2015).

Related publications:

Hughes, A.N. (2020), Mechanical controls on structural styles in shortening environments: A discrete-element modeling approach, in Hammerstein, J.A., Di Cuia, R., Cottam, M., Zamora, G., and Butler, R.W.H., eds., Fold and thrust belts: Structural Style, Evolution and Exploration, Geological Society of London, Special Publications 490. Link

Hughes, A.N., and J.H. Shaw, (2015) Insights into the mechanics of fault-propagation folding styles, Geological Society of America Bulletin, v. 127 (11-12), p. 1752-1765. Link

Hughes, A.N., N.P. Benesh, and J.H. Shaw, (2014), Factors that control the development of fault-bend versus fault-propagation folds: Insights from mechanical models based on the discrete element method (DEM), Journal of Structural Geology, 68A, p. 121-141. Link